Double deflation: Double Distilled or Double Dutch? Some remarks about the estimation of real economic production – Part 1
Download the WEA commentaries issue ›
This piece benefitted from remarks of Stuart Birks, Diane Coyle and Josh Mason
Much of empirical macro-economics can be described as the science of complicated weighted averages. Statisticians take great care to use the right weights. But choices have to be made. This article will argue that the weights chosen as well as the aggregation procedures used influence the level and growth rates of macro-economic variables. As such, this is not disputed among specialists. The article will however also argue that calculation of ‘real’ variables like economic growth, though useful, are just that: calculations. We should take care not to conflate ‘deflated’ nominal variables with real flows of goods and services.
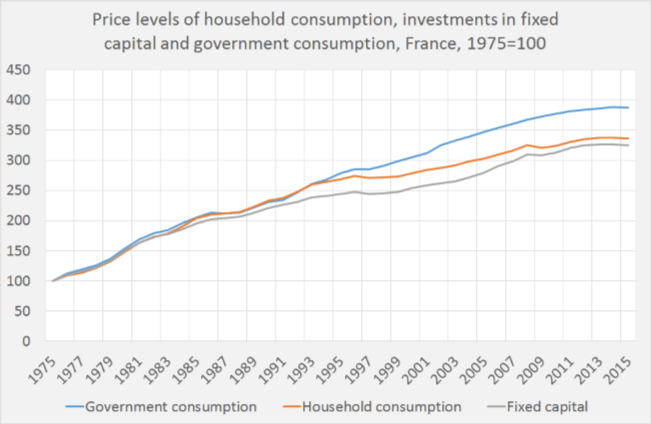
Economists estimate the national accounts, which contain interrelated sectoral monetary flows of income, production and expenditure in current prices. These estimates are also used to calculate what is called ‘real’ production, expenditure and income. The phrase ‘real’ means that effects of prices changes are filtered out of the estimates, to be able to gauge how the volume of the aforementioned variables has developed. Have we not only become richer or more prosperous in a nominal sense but also when we look at the amount of goods and services which are available? And did productivity go up? There are standard methods to do this (Eurostat, 2015). Have these methods inherent biases? Or does misunderstanding about these often little known procedures, like ‘double deflation’, also bias our understanding of the data? This article will argue that we have to take care with ‘real’ data as there are, depending on the method chosen, different aspects of reality. An important reason to take care is that the convenient, influential and often quite implicit assumption in many macro models of one macro consumption/investment good and one macro price is too complacent. As the statistics show (see graph), French prices of fixed investment goods (new buildings, machinery, transport equipment) rose, in the long run, quite a bit less than the price of government consumption (education, justice, police). Government consumption has of course, unlike most investment goods, no market price, see Eurostat, 2015, for more precise definition of how the price level of for instance education is estimated. As prices define, together with quantities, the value of specific goods and services and as the monetary value of goods and services is, ultimately, the most important variable influencing the weight given to such a good or service when estimating the national accounts in nominal prices or calculating ‘real’ production, this difference in the development of the price level also means that the weights of government consumption in total production and expenditure increases. While the weight of for instance computers decreases. It is even possible that computers, despite the surge in sales, nowadays have a lower weight than for instance education, even when the volume of education might have declined a little! Such developments differences are interesting to economists and instead of assuming them away with the ‘one good’ assumption economists should embrace them. But to be able to do this, we have to know a little about the arcane ways, like the double deflation method, used to estimate the differences and about how this influences the variables measured and calculated.1
Restating the problem and turning from expenditure and production to income: when your paycheck increases but prices increase faster, the purchasing power of your income declines. Economists try to estimate this decline by correcting your ‘pay cheque income’ for this change in prices. To do this, they use price indices based upon weighted averages of a large number of individual prices. Obviously, the weights used have to be relevant. Which one can doubt. In 2015, Scott Sumner wrote a blogpost about: ‘The bizarre way economists calculate real income’. He was dumbstruck about the price indices used to ‘deflate’ disposable income. ‘Deflation’ means that a nominal series is divided by a price index to obtain a ‘real’ series. There are quite a bunch of different indices and it seemed to him as if economists did not care about the choice of the right index, sometimes even leaving prices of investment goods out of the deflation procedure of GDP, which includes investment expenditure and the production of investment goods. Sumner was right – but doing this is consistent with the one good macro models! His was not a critique of the price indices – but of the loose way economists use these. A year later Yanis Varoufakis wrote a blogpost about the situation in Greece, where nominal production declined but real production increased: deflation.2 He put forward different arguments but came to a somewhat comparable conclusion as Sumner: we have to take care when interpreting a calculated variable. And it’s not just these two rogue economists. Recently, the IMF voiced the same warning: “A volume estimate of GDP is an essential measure of economic activity because it removes the effects of price changes. The System of National Accounts 2008 (2008 SNA) recommends a technique called double deflation. In contrast, single deflation, the deflation with a single price index, is not recommended because it fails to capture important relative price changes” (Alexander e.a., 2017). Clearly, care has to be taken while it is not just about increases and decreases of prices but also about relative changes of prices. And the IMF even seems to aim at ‘double deflated’ statistics… Why is everybody so concerned?
The basic problem is that nominal production is a function of ever changing prices and ever changing quantities, changes which also affect relative prices and quantities. Economic models circumvent this idea by supposing one good which has one price. No problems there with changing relative prices and quantities! Shifting the focus somewhat: the same holds for the ‘representative consumer’. A price index for the elderly and a price index for young parents might develop differently. But the idea of one good and a single ‘representative consumer’ enables economists to circumvent such complications (though it has to be admitted that the representative consumer is getting less popular). In reality, ever changing (relative) prices are a ‘fact of life’ and statisticians try to capture this ‘Alice in wonderland’ world.3 Their problem however – using fixed prices to estimate production (or expenditure or whatever) by definition freezes one set of relative prices. When we state: ‘In 2016 the volume of Italian Gross Domestic product (GDP) increased by 1.1%’ we ‘deflate’ nominal prices with a price index and basically state that the amount of products and services produced was 1.1% larger than in 2015, using a specific set of weights. Which means that estimates of ‘real’ production (as well as real expenditure and income) are not uniquely defined. There is of course quite an amount of ‘scientific discipline’ behind the methods used to obtain the weights used to construct a ‘deflator’, i.e. a price index used to change a nominal value into a real value (a Törnqvist index, anyone?). But that does not solve the real problem. As relative prices as well as quantities change this means that taking one year instead of another to choose the weights for the individual prices will lead to another value of the price index.
To overcome part of the problem economists have developed the methodology of ‘Double Deflation’ (Alexander e.a., 2017; Eurostat 2015). To understand this method, one has to realize that GDP and the national accounts are all about Value Added, i.e. the monetary value of output (say: of milk and meat) minus the value of purchased inputs (say: feed and artificial fertilizer). This value added is the amount of money available to pay incomes (wages, profits, rents). The double deflation method does not deflate this value added directly with one price index but deflates the nominal value of total outputs with an index based upon output prices and the nominal value of total inputs with an index of input prices. Real input is consequently subtracted from real output and the result is real value added. are separately deflated, with different price indices. In the literature, one can find scores of articles which argue that Double Deflation is superior to single deflation when wants to know the value of ‘real’ GDP (Alexis e.a., 2017 for further references).
This is where the confusion starts. It’s not in my Ph. D. but I remember that, working on my calculations, it showed that applying double deflation to the value added of Dutch agriculture, using 1880 prices of outputs and inputs, led to negative real value added while at the same time nominal incomes were positive. This was possible as after 1880 prices of inputs (feedcakes and grains, artificial fertilizer) plummeted relative to output prices, which (together with other developments, Knibbe, 1993) lead to an upsurge in their use. The amazing volume increase of purchased inputs which I calculated was ‘real’. The considerable but much smaller volume increase of outputs was also ‘real’. But subtracting the value of inputs in 1880 prices from the value of output in the same prices was, for later years, bonkers. Relative prices had changed too much to be able to do this (more formal about this: Dietzenbacher and Hoen, 1999). In the short run, this is less of a problem. But where does the short run stop and the long run begin? In a technical sense this is a problem which can approximately be solved by using a Törnqvist index. But that’s not the point. Any deflator is subject to a weights problem. Which means that double deflation is doubly susceptible to this problem or in fact, when we realize that we are in fact using the relation of one deflator to another which is also a historical construct, triply susceptible. That’s not a bad thing as the changes of the weights indicate how our lives and economies have changed. That’s the interesting thing about such calculations.
This does not just hold for production estimates. Double deflation might, using a nifty index, be right for production estimates. But when you want to estimate real income, single deflation of incomes or deflating nominal value added with a price index is best. Though, taking some inspiration from Sumner, it is of course obvious that such a price index should, in the case of farm income, also contain prices of investment goods. An example (from my Ph. D. thesis): according to my production estimates, Dutch farmers did well in the twenties. Production and productivity increased. But at the same time farmers did at the time clearly not agree with such a rosy view of the development of agricultural production (and the farmers view for a long time dominated our view of agricultural development in the Netherlands in this period). The consumer price index rose faster/declined less than the price index of agricultural products and nominal value added deflated by the consumer price index actually declined (after 1921). More production (actually: more ‘real’ agricultural value added could buy less goods and services. Both estimates are true. Purchasing power of farmers’ incomes declined. But ‘real’ value added increased or, to state this in another way, the amount of agricultural goods available to ‘the rest’ of the economy did not only increase but also became relatively cheaper; the terms of trade of agriculture deteriorated.
Adding some complexity to this: value added is the amount of income available for entrepreneurs (including the self-employed), wage earners and providers of capital. Before deflating it, it might be broken down into its constituent parts: wages, profits and rents (as well as the fuzzy variable ‘mixed income’ of the self-employed). Wages might be deflated with the price index (though Sumner does remark, more or less, that consumption is not just financed with wage income). Entrepreneurs, the self-employed and providers of (real) capital however also use the money to invest. Which means that there is an argument to deflate nominal value added with a price index which is a weighted average of the consumer price index and the investment goods price index. The GDP-deflator comes close. But investments are much more volatile than consumer spending. Which leads to even more weight-problems. To state this more precisely: this leads to even more problems when we accept the too convenient assumption that the economy produces only one good but to even more possibilities to analyze the economy and to investigate what changes when we understand price indices a little better: counterfactuals of actual events.
In the next piece I will show how different methods lead to different results, pay some attention to institutional influences on prices, like indirect taxes and discuss how the problems mentioned here should influence policy variables like the inflation targets of central banks.
Alexander, Thomas, Claudia Dziobek, Marco Marini, Eric Metreau, and Michael Stanger (2017) Measure up: A Better Way to Calculate GDP. IMF Staff discussion note 17/02
Dietzenbacher, E and A.R. Hoen, ‘Double deflation and aggregation’. Environment and Planning A, volume 31, pp. 1695-1704
Eurostat (November 3, 2015), Statistics Explained. Building the System of National Accounts – volume measures. Available here.
Knibbe, Merijn (1993). Agriculture in the Netherlands 1851-1950. Production and institutional change. Amsterdam: NEHA.
__________________________
- Economists have their own way with language and the names of variables. It is remarkable that the value of a calculated variable which is based upon prices not actually paid is called ‘real’ while the value of the nominal variable, which is actually estimated and based upon prices which were paid, is supposedly ‘not real’.
- As stated, economists have their own way with language. ‘Deflation’ is a procedure to correct nominal series for price changes by dividing them by a price index. But is also a noun describing a situation where the general price level is declining.
- The classical reference is ‘The Gerschenkron effect’, which also encompasses the idea that Shumpeterian dynamics lead to large volume growth as well as large price declines of successful new products – ‘Wonderland’ like changes of frames of reference are not random.
From: pp.12-15 of WEA Commentaries 7(1), February 2017
http://www.worldeconomicsassociation.org/files/Issue7-1.pdf